url <- "https://raw.githubusercontent.com/milesdwilliams15/Teaching/main/DPR%20201/Data/aidExperiment.csv"
Data <- read_csv(url)12 Randomized Experiments
12.1 Goals
- Randomized experiments provide the best way to make causal inferences.
- The randomization process helps us avoid the problem of bias or confounding in our data.
- We have lots of tools in R for doing randomization and estimating treatment effects.
- There are many kinds of estimators of treatment effects, including the average treatment effect (ATE), the intent to treat effect (ITT), and the compliers average treatment affect (CATE).
You’ll need the following packages in your environment to follow along with the notes:
library(tidyverse)
library(socsci)
library(here)
library(estimatr)
library(randomizr)12.2 Why Randomized Controlled Trias?
A randomized controlled trial (RCT) is a research design that allows us to obtain unbaised estimates of a treatment effect or other target estimand. The randomization process, when done correctly, is the only method we have to ensure that getting some treatment or policy intervention is independent of both observed and unobserved factors that might bias our analysis.
Think of it this way. The world is a complicated place, with lots of known and unknown factors that can bring about different relationships between factors in the world. Take the correlation between a country being a major oil exporter and the kind of governance style in that country. It’s true that countries where oil is more than 50% of their exports also tend to be autocratic. But how can we know whether this relationship is causal? If we could flip a switch and make the oil stop flowing in these countries, do we think we could turn them into democracies? Maybe. But there could be other, deep historical reasons why these countries remain autocratic as well, and these factors could also be correlated with geography and natural resources, such as oil. So it’s hard to say that this one change is sufficient to bring about democracy.
Questions like this are hard to find good answers to, but they are important to ask. In the world of politics and policy, before we think about how we would want to intervene in the world to make it a better place, we need to think seriously about how confident we are that X intervention will lead to Y outcome. Shutting off the flow of oil in an autocratic country is probably beyond our reach, but there are many hypothetical and realistic policy interventions that we can consider nearer to home. Will body cams lead to better policing? Will increasing the minimum wage improve the standard of living for many people? Are progressive tax systems a reliable means of supporting public services that benefit the lower and middle classes? Could a proportional voting system better the chances of third parties in US politics?
Not all of these questions can be realistically answered using randomized experiments, but using the logic of a randomized experiment can help discipline our thinking. What kind of evidence would we need to feel confident that a proposed policy intervention or change will have the desired outcome? If we propose a policy, even a pie-in-the-sky policy, we should want to ground our recommendation in evidence to whether it will be effective. Randomized controlled trials are the first kind of research design we should try to consider.
We talked a little bit about how randomization is important for making causal inferences in the last couple of chapters. However, there are many different ways to go about randomization. While RCTs are a unique kind of research design, there is lot of diversity among RCTs in terms of how units in our study are assigned to treatment or control. In the next section, we’ll use the {randomizr} R package to walk through a few different techniques. These include simple randomization, complete randomization, block randomization, and cluster randomization.
Then, for each one of these methods, we’ll walk through how we would analyze the results of an RCT based on the randomization strategy we choose. The key mantra we’ll emphasize is “analyze how you randomize.”
Okay, let’s get to it.
12.3 Random Treatment Assignment with {randomizr}
The {randomizr} package was created to give researchers doing field, lab, survey, or online experiments tools to automate the process of random assignment. You can read more about the package here: https://declaredesign.org/r/randomizr/.
The package provides functions that make it easy to implement randomization according to five different common research designs:
- Simple randomization
- Complete randomization
- Block randomization
- Cluster randomization
- Block-cluster randomization
To keep things simple, we’ll focus on the first four. Also, for each we’ll consider scenarios where there are only two treatment conditions (that is, treatment or control). There are many studies that rely on multiple treatment conditions. We sometimes call these multi-arm treatments. These might look like variations of a treatment condition or versions of a treatment with a different dose. There are also factorial designs where there are multiple treatments but it is possible for one unit to fall into more than one treatment condition at once. However, before you start thinking about these additional research designs, it’s important to master the basics first.
For each of these kinds of randomization, we’re going simulate an experiment based on some actual data:
Take a glimpse at the data:
glimpse(Data)Rows: 1,289
Columns: 12
$ aid <dbl> 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0…
$ gender <dbl> 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0…
$ educ <dbl> 3, 5, 3, 3, 3, 2, 3, 5, 5, 5, 5, 5, 2, 3, 6, 5, 2, 3, 6, 2…
$ relimp <dbl> 2, 4, 3, 3, 4, 2, 2, 1, 3, 1, 1, 4, 3, 3, 2, 1, 3, 1, 1, 3…
$ treat_cash <dbl> 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1…
$ treat_black <dbl> 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1…
$ loinc <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ age <dbl> 28, 37, 68, 55, 71, 69, 73, 58, 66, 43, 42, 40, 79, 59, 61…
$ fullemploy <dbl> 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1…
$ ties3 <dbl> 0, 1, 2, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 2, 0, 0, 0, 1, 1…
$ lib <dbl> 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0…
$ race3 <dbl> 1, 1, 3, 1, 1, 1, 1, NA, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, …There are some real treatments in this data, but we’ll ignore these for now.
The data comes from this study published in 2020 in International Studies Quarterly that looks at support for foreign aid by the American public. The aid column equals “1” if an individual supports a foreign aid project and “0” if they don’t. The other columns provide some other background information about individual respondents.
12.3.1 Simple randomization
As the name implies, simple randomization involves just assigning each individual in the data the same probability of getting treatment and then letting a random number generate do its thing. The relevant function is simple_ra():
Data |>
mutate(
simpleTr = simple_ra(N = n())
) -> DataThe thing about simple randomization is that we can end up, by random chance, with unequally sized treatment and control groups:
table(Data$simpleTr)
0 1
613 676 Maybe that’s no big deal, but in some cases we may have a fixed number of available treatments. Think about something like letters in the Montana Wildfires study we discussed before. There were a set number of letters budgeted to be sent out. So no matter the luck of the draw, exactly the same number of people will get the treatment. When this is the case, we need to use complete randomization.
12.3.2 Complete Randomization
We use complete_ra() for complete randomization:
Data |>
mutate(
completeTr = complete_ra(N = n())
) -> DataThis approach will by default give us equal (or almost equal if our data has an odd number of rows) treatment and control groups:
table(Data$completeTr)
0 1
645 644 If we want to control the number of individuals who get treatment, we can just modify the m = command:
Data |>
mutate(
completeTr = complete_ra(N = n(),
m = 500)
) -> DataNow there are only 500 treated individuals:
table(Data$completeTr)
0 1
789 500 12.3.3 Block Randomization
The beauty of randomized experiments is that, in principle, treatment assignment is independent of observed and unobserved factors that might bias our analysis. But in practice we can still get imbalances between treatment and control groups due purely to random chance. Maybe this is no big deal, but it could be a problem if treated and control individuals also differ on a covariate that might influence the outcome we’re interested in studying.
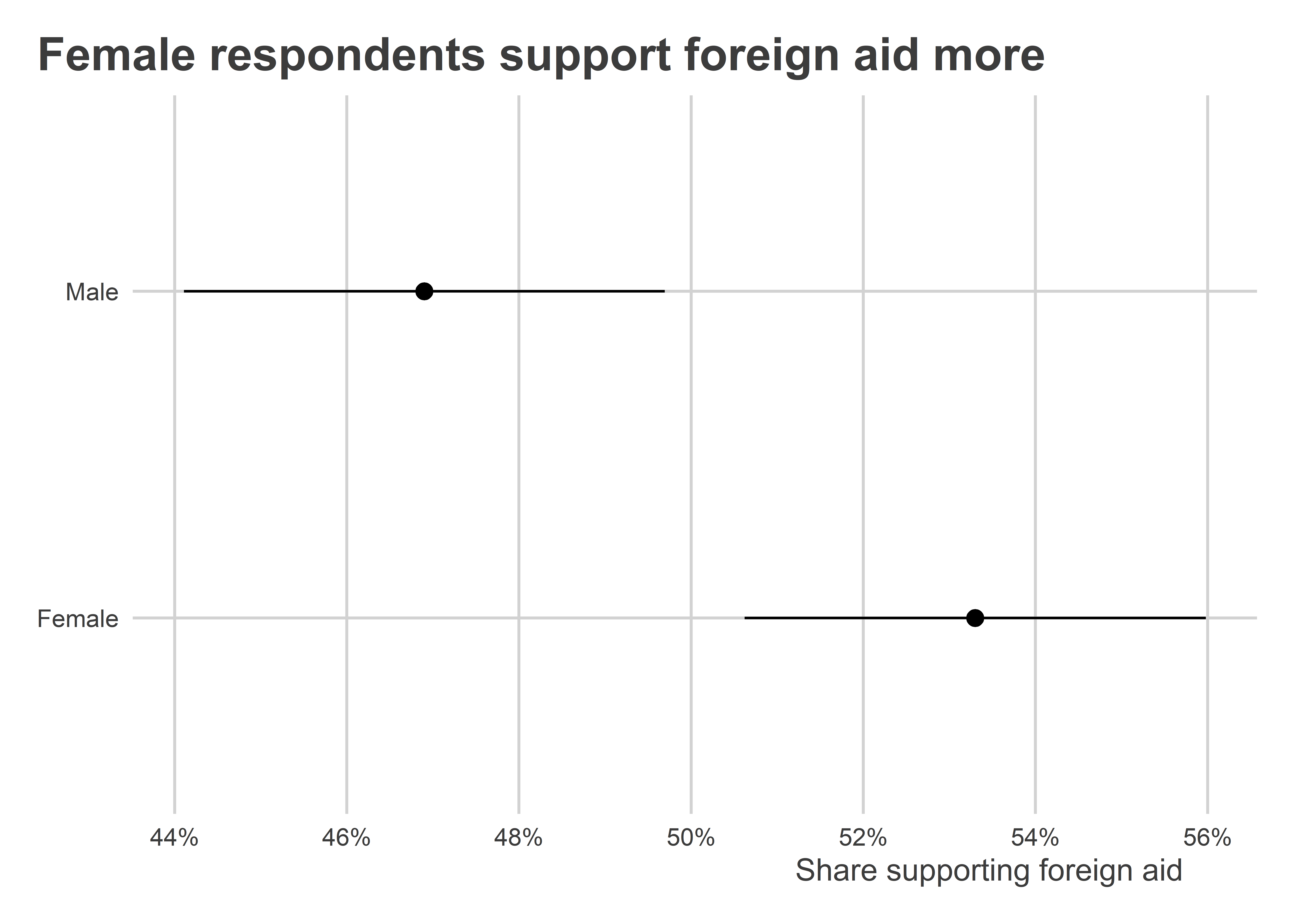
For example, if we look at the relationship between gender and support for foreign aid, women are more likely than men to indicate that they support foreign aid. If we happen to have more female respondents in our treatment condition but more male respondents in the control condition, we might run the risk of over-estimating the size of the treatment effect.
Data |>
group_by(gender) |>
mean_ci(aid) |>
ggplot() +
aes(x = mean,
xmin = mean - 1.39 * se,
xmax = mean + 1.39 * se,
y = ifelse(gender==1, "Female", "Male")) +
geom_pointrange() +
scale_x_continuous(
labels = scales::percent,
n.breaks = 6
) +
labs(
x = "Share supporting foreign aid",
y = NULL,
title = "Female respondents support foreign aid more"
)
If we’re worried about this happening we can turn to a technique called block randomization, or what some researchers call stratified randomization. The idea is to randomize treatment within a specific group rather than across the whole data regardless of unit characteistics. In the case of our hypothetical research study, a good strategy is block randomize based on gender to ensure we have equal numbers of treated male and female respondents. We can do this with block_ra():
Data |>
mutate(
blockTr = block_ra(blocks = gender)
) -> DataCheck it out:
Data |>
group_by(gender) |>
ct(blockTr)# A tibble: 4 × 4
# Groups: gender [2]
gender blockTr n pct
<dbl> <int> <int> <dbl>
1 0 0 309 0.5
2 0 1 309 0.5
3 1 0 336 0.501
4 1 1 335 0.499Compare this with what we got with complete random assignment. As you can see, there’s some notable discrepancies between the genders and treatment versus control conditions. Since gender clearly explains values of the outcome variable of interest, we could inadvertently generate misleading results about the treatment effect. But, by ensuring an equal number of males and females receive treatment, we can avoid this problem.
Data |>
group_by(gender) |>
ct(completeTr)# A tibble: 4 × 4
# Groups: gender [2]
gender completeTr n pct
<dbl> <int> <int> <dbl>
1 0 0 378 0.612
2 0 1 240 0.388
3 1 0 411 0.613
4 1 1 260 0.387We can also block randomize on multiple categories, say gender and race:
Data |>
mutate(
blockTr = block_ra(blocks = paste(gender, race3))
) -> DataThe beauty with this approach is that we can get really specific about how we want to, ahead of time, effectively control for different factors in our RCT. The main limitation with block-randomization, however, is that we can only block on factors that we have in our data. If we’re concerned that variable X will influence our outcome and we want to be sure that we don’t get a disproportionate number of observations with characteristic X in either our control or treatment group, we should try really hard to ensure we collect data on X before we randomize.
All of this data that we collect about our observations is what we call pre-treatment data. We call it this because we collect information about it before we give treatment. Data collected after treatment is called post-treatment. This distinction seems trivial now, but when we talk about other kinds of research designs (such as selection on observables in the next chapter), we have to be careful about whether the factors we adjust for in our analysis are pre- or post-treatment.
12.3.4 Cluster Assignment
Cluster randomization involves randomizing, not at the level of individuals or within blocks, but instead at the level of groups or clusters.
A classic example of a clustered design is an experiment involving classrooms in a school. Some studies looking at the effect of curriculum or teacher characteristics follow a clustered research design for logistical reasons. It often is impossible to offer different students in the same classroom different interventions. Instead, researchers will have to assign whole classrooms to different interventions.
The cluster_ra() function does cluster randomization. For the sake of example, say we clustered treatment by education in our foreign aid study. Here’s how we’d do it.
Data |>
mutate(
clusterTr = cluster_ra(clusters = educ)
) -> DataNotice that individuals in different education categories have either all gotten treatment or all been assigned to the control condition:
Data |>
group_by(educ) |>
ct(clusterTr)# A tibble: 6 × 4
# Groups: educ [6]
educ clusterTr n pct
<dbl> <int> <int> <dbl>
1 1 0 42 1
2 2 1 467 1
3 3 0 296 1
4 4 0 122 1
5 5 1 228 1
6 6 1 134 1It practice, clustering on education would make no sense, but for the sake of showing how the function works, there you go.
We could also imagine that individuals who took our survey were from different cities and we could only implement our intervention at the level of cities, as would be the case with a public messaging intervention, for example:
Data |>
mutate(
city = sample(LETTERS[1:10], n(), T),
clusterTr = cluster_ra(clusters = city)
) -> DataCheck it out:
Data |>
group_by(city) |>
ct(clusterTr)# A tibble: 10 × 4
# Groups: city [10]
city clusterTr n pct
<chr> <int> <int> <dbl>
1 A 0 134 1
2 B 0 122 1
3 C 1 123 1
4 D 0 138 1
5 E 1 134 1
6 F 1 129 1
7 G 1 140 1
8 H 0 124 1
9 I 0 118 1
10 J 1 127 112.4 Analyze How You Randomize
The average treatment effect (ATE) is a pretty simple estimator of causal effects. Just take the difference in means between treated and control groups. However, the process of estimating the ATE can become a little more involved depending on the kind of RCT we use in our study. For simple and complete randomization designs, a simple difference in means estimator is sufficient. However, for block and cluster randomized designs we need to do a few extra things to ensure we minimize bias or errors in our estimate of the ATE.
The rule of thumb is to analyze how your randomize. The following examples demonstrate how you would estimate the ATE depending on which kind of randomization approach you used.
12.4.1 Simple and complete randomization
This one is pretty easy, and it’s exactly what we did in the previous chapter when we talked about tools in R for estimating causal effects. We can just use lm_robust() like so with simple randomization:
lm_robust(aid ~ simpleTr, data = Data) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.51223491 0.02020525 25.3515747 2.521187e-115 0.47259604
simpleTr -0.01890158 0.02791247 -0.6771732 4.984179e-01 -0.07366055
CI Upper DF
(Intercept) 0.5518738 1286
simpleTr 0.0358574 1286We can do exactly the same with complete randomization:
lm_robust(aid ~ completeTr, data = Data) Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper
(Intercept) 0.500 0.01782308 28.0535203 1.681085e-135 0.46503451 0.53496549
completeTr 0.006 0.02861104 0.2097092 8.339278e-01 -0.05012944 0.06212944
DF
(Intercept) 1286
completeTr 1286This is really simple, right? Keep this in mind when or if you happen to be in a position to design an RCT in the future, because this kind of randomization is dead-simple to analyze.
12.4.2 Block randomization
If we block randomized, we can technically apply the same approach as above, but it is recommended that we instead calculate the average treatment effect within blocks. This technically is a weighted version of the ATE.
The value of accounting for blocks in the analysis becomes increasingly important to the extent that the blocks are of different sizes and individuals within blocks had different probabilities of being assigned to treatment.
The standard approach for some time has been to just add block fixed effects to our regression model, which can be done with lm_robust() like so:
lm_robust(aid ~ blockTr,
fixed_effects = ~ gender,
data = Data) Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
blockTr 0.03862279 0.02781947 1.388337 0.1652751 -0.01595377 0.09319936 1285But some research has shown that this approach can sometimes give us inappropriate weights and actually bias our estimate of the ATE. The reason is that some blocks can be outliers, and the ATE for these blocks could drive up or down our estimate of the ATE.
As an alternative, we can use a method called the Lin Estimator. This approach involves interacting the treatment with blocks or strata after mean centering them. It’s a technical read, but you can read more about the justification of this approach by reading this 2013 study by Winston Lin where he proposes this method. The Lin estimator is also the approach that the US Office of Evaluation Sciences recommends as its default for block randomized studies (link: https://oes.gsa.gov/assets/files/block-randomization.pdf).
This can be an involved process, but the lm_lin() function from {estimatr} makes using the Lin Estimator easy. Just write:
lm_lin(aid ~ blockTr,
covariates = ~ gender,
data = Data) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.48299367 0.01969955 24.5180071 3.344048e-109 0.44434683
blockTr 0.03862278 0.02782693 1.3879643 1.653887e-01 -0.01596845
gender_c 0.04792351 0.03942098 1.2156855 2.243282e-01 -0.02941309
blockTr:gender_c 0.03108082 0.05570280 0.5579759 5.769581e-01 -0.07819767
CI Upper DF
(Intercept) 0.52164051 1284
blockTr 0.09321402 1284
gender_c 0.12526010 1284
blockTr:gender_c 0.14035931 1284The estimate for blockTR is the estimate of the ATE.
12.4.3 Cluster randomization
When we use a cluster randomized design, we don’t need to add special fixed effects, but we do need to change the way we calculate our standard errors. The reason is that uncertainty that comes from random assignment is not at the individual level but at the level of clusters. Remember the sharp null hypothesis? To make causal inferences with the sharp null as our reference point, we are trying to imagine what different sets of ATEs we could have estimated by giving treatment to different units. In a cluster randomized trial we didn’t just give treatment to different units; we gave it to different groups of units. So when we make an inference to the sharp null, we want to consider what set of ATEs we could have gotten by assigning treatment to different groups (not just individuals).
That means that we want our standard errors to capture uncertainty, not from shaking up which individuals got treatment, but instead by shaking up which clusters got treatment. To ensure we do this, we can use a kind of standard error called a cluster-robust standard error. This lets us approximate this kind of inference, and it’s quite easy to do with lm_robust() using the cluster option. Here’s an example with the clustered treatment that we assigned by hypothetical cities in the data:
lm_robust(aid ~ clusterTr, data = Data,
clusters = city) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.50786164 0.01584218 32.0575500 5.869996e-06 0.46380515
clusterTr -0.01092912 0.02942780 -0.3713876 7.200239e-01 -0.07882975
CI Upper DF
(Intercept) 0.55191812 3.983595
clusterTr 0.05697152 7.97300912.5 The ITT and CATE
Sometimes people don’t comply with our experimental designs. This can influence the results of our studies, but under the right conditions, we can adjust for noncompliance.
People can fall into one of four different categories:
- Compliers: People that follow the treatment given.
- Always-takers: People that always are treated no matter their assignment.
- Never-takers: People that never are treated no matter their assignment.
- Defiers: People that always do the opposite of what they are assigned.
Remember the get-out-the-vote experiment we talked about several weeks ago:
url <- "https://raw.githubusercontent.com/milesdwilliams15/Teaching/main/DPR%20201/Data/GOTV_Experiment.csv"
gotv <- read_csv(url)
glimpse(gotv)Rows: 50,000
Columns: 9
$ female <dbl> 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,…
$ age <dbl> 34, 37, 43, 45, 47, 45, 57, 20, 30, 25, 36, 27, 25…
$ white <dbl> 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0,…
$ black <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1,…
$ employed <dbl> 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1,…
$ urban <dbl> 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1,…
$ treatmentattempt <dbl> 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0,…
$ successfultreatment <dbl> 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0,…
$ turnout <dbl> 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1,…Not all individuals in the data who were randomly assigned to get a get-out-the-vote phone call actually picked up the phone. To put a precise number on it:
complied <- mean(gotv$successfultreatment[gotv$treatmentattempt==1])
complied[1] 0.7688753That means that in the data we have a 77% compliance rate with the treatment.
We can use this information to recover a special kind of causal estimate called the compliers average treatment effect or CATE. To calculate it, we first need to calculate something else called the intention to treat effect or ITT.
The ITT is actually calculated the same as the ATE, but since we know that we have noncompliers in the data the estimate has a conceptually different interpretation:
ITT <- coef(lm(turnout ~ treatmentattempt, gotv))[2]
ITTtreatmentattempt
0.07098882 The ITT is the product of a couple of different things: (1) the compliance rate and (2) the CATE: \[\text{ITT} = c \times \text{CATE}\]
Using some simple algebra, we can take our known quantities of ITT and the compliance rate c to recover the CATE estimate. \[\text{CATE} = \frac{\text{ITT}}{c}\]
So in R we would just write:
CATE <- ITT / complied
CATEtreatmentattempt
0.09232814 We can get this same estimate using regression. Specifically, instrumental variables regression. This approach involves a two-stage process of arriving at the CATE. The function iv_robust() from {estimatr} takes care of these steps for us. We just need to give it a slightly different way of writing a formula than we’ve done up to now:
iv_robust(turnout ~ successfultreatment | treatmentattempt,
data = gotv) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.48467348 0.003176074 152.60146 0.000000e+00 0.47844834
successfultreatment 0.09231023 0.005788652 15.94676 4.159227e-57 0.08096441
CI Upper DF
(Intercept) 0.4908986 49740
successfultreatment 0.1036561 49740See how the coefficient for successfultreatment is identical to the one we previously calculated.
Notice that this isn’t the same thing as just doing this:
lm_robust(turnout ~ successfultreatment,
data = gotv) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.4742721 0.002857794 165.95741 0.000000e+00 0.4686707
successfultreatment 0.1192421 0.004552561 26.19231 3.412514e-150 0.1103190
CI Upper DF
(Intercept) 0.4798734 49740
successfultreatment 0.1281652 49740To show what’s going on here, I’ll use lm() and break the process down. It involves two stages.
In stage 1, we first need to estimate the relationship between treatment assignment and treatment compliance:
stage1_fit <- lm(successfultreatment ~ treatmentattempt, gotv)There should be a significant relationship between the two:
summary(stage1_fit)
Call:
lm(formula = successfultreatment ~ treatmentattempt, data = gotv)
Residuals:
Min 1Q Median 3Q Max
-0.7689 0.0000 0.0000 0.2311 0.2311
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.199e-13 1.893e-03 0.0 1
treatmentattempt 7.689e-01 2.671e-03 287.8 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2987 on 49998 degrees of freedom
Multiple R-squared: 0.6236, Adjusted R-squared: 0.6236
F-statistic: 8.283e+04 on 1 and 49998 DF, p-value: < 2.2e-16In stage 2, we’ll do something clever. Rather than look at the relationship between successful treatment and turnout, we’ll look at the relationship between predicted successful treatment and turnout:
stage2_fit <- lm(turnout ~ predict(stage1_fit), gotv)
summary(stage2_fit)
Call:
lm(formula = turnout ~ predict(stage1_fit), data = gotv)
Residuals:
Min 1Q Median 3Q Max
-0.5557 -0.4847 0.4443 0.4443 0.5153
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.484673 0.003167 153.04 <2e-16 ***
predict(stage1_fit) 0.092328 0.005812 15.88 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4983 on 49740 degrees of freedom
(258 observations deleted due to missingness)
Multiple R-squared: 0.005048, Adjusted R-squared: 0.005028
F-statistic: 252.3 on 1 and 49740 DF, p-value: < 2.2e-16This coefficient is identical to the CATE we got before. Importantly, the standard error from this approach is incorrect. The reason is that the first-stage predictions used in the second-stage model are estimates. That means that the classical OLS standard errors aren’t going to capture all the relevant uncertainty in the data. Thankfully, iv_robust() takes care of this for us and reports the correct standard errors.
Another nice feature of the regression approach to estimating the CATE is that it can accommodate controlling for covariates. For example, say we want to account for urban/rural status as we estimate the CATE. We can specify our regression model as follows:
iv_robust(turnout ~ successfultreatment + urban | treatmentattempt + urban,
data = gotv) Estimate Std. Error t value Pr(>|t|) CI Lower
(Intercept) 0.52966399 0.005518537 95.979063 0.000000e+00 0.51884759
successfultreatment 0.04842280 0.007313844 6.620704 3.611159e-11 0.03408758
urban -0.05639415 0.005625235 -10.025207 1.243799e-23 -0.06741967
CI Upper DF
(Intercept) 0.54048038 49739
successfultreatment 0.06275802 49739
urban -0.04536862 49739Note that you must include the same covariates on both sides of the | that you want to control for.
12.6 Checking Balance and (Non)Random Attrition
Sometimes in our studies, experiments break. This was certainly the case in the GOTV experiment which generated the data above. A sign that something has gone wrong is when treatment and control groups differ substantially on observed covariates.
To assess balance quickly, we can get lm_robust() to tell us how much our covariates differ by treatment. Notice the use of cbind() on the left-hand side of the equation. This code forces lm_robust() to report the average difference in each of the covariates specified inside cbind() based on treatment. It then pipes the data into some code that produces a coefficient plot based on the results.
## First, regress each covariate on treatment assignment
lm_robust(cbind(female, age, white,
black, employed, urban) ~ treatmentattempt,
data = gotv) |>
## tidy the results
tidy() |>
filter(term != "(Intercept)") |>
## plot
ggplot() +
aes(x = estimate,
xmin = conf.low,
xmax = conf.high,
y = outcome) +
geom_pointrange(size = .1) +
geom_vline(xintercept = 0, lty = 2) +
labs(x = "Difference relative to control",
y = NULL,
title = "Covariate Balance between Treatment and Control")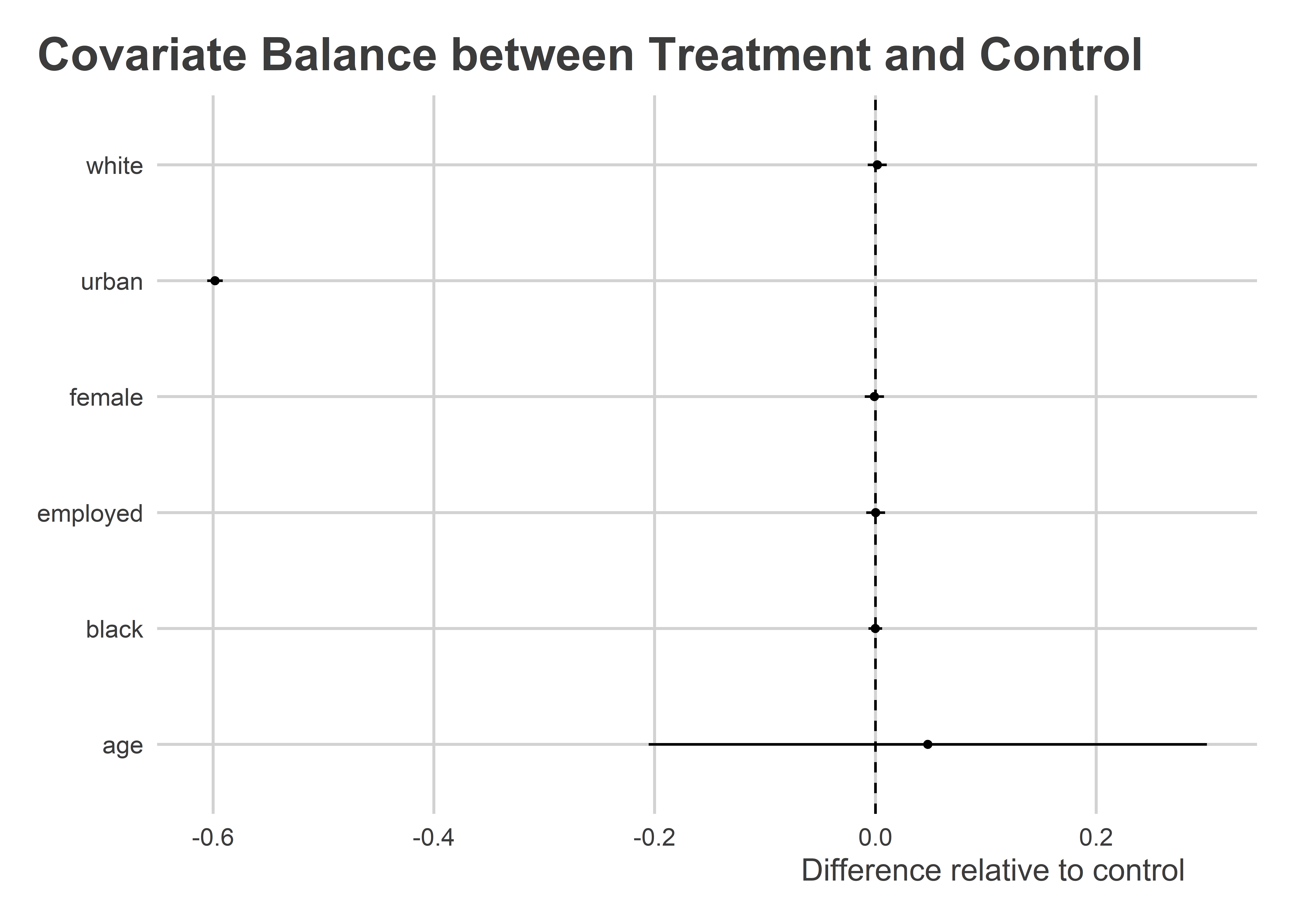
Wow! It looks like people in urban settings were unusually unlikely to be in the treatment condition. If urban status is important for predicting turnout (which it is), that’s a problem.
Attrition can be a problem in experiments, too. In this same experiment, we have missing data for 258 individuals regarding whether they turned out to vote. Is missingness correlated with other characteristics of respondents? Yes, as a matter of fact. Both non-white and younger respondents were more likely to have missing values for turnout. This could also bias estimates for the effect of the GOTV campaign.
lm_robust(
is.na(turnout) ~ female + age + white + black + employed + urban,
data = gotv
) |>
tidy() |>
filter(term != "(Intercept)") |>
ggplot() +
aes(x = estimate,
xmin = conf.low,
xmax = conf.high,
y = term) +
geom_pointrange(size = .1) +
labs(x = "Coefficient",
y = NULL,
title = "Who has missing turnout data?") +
geom_vline(xintercept = 0,
lty = 2)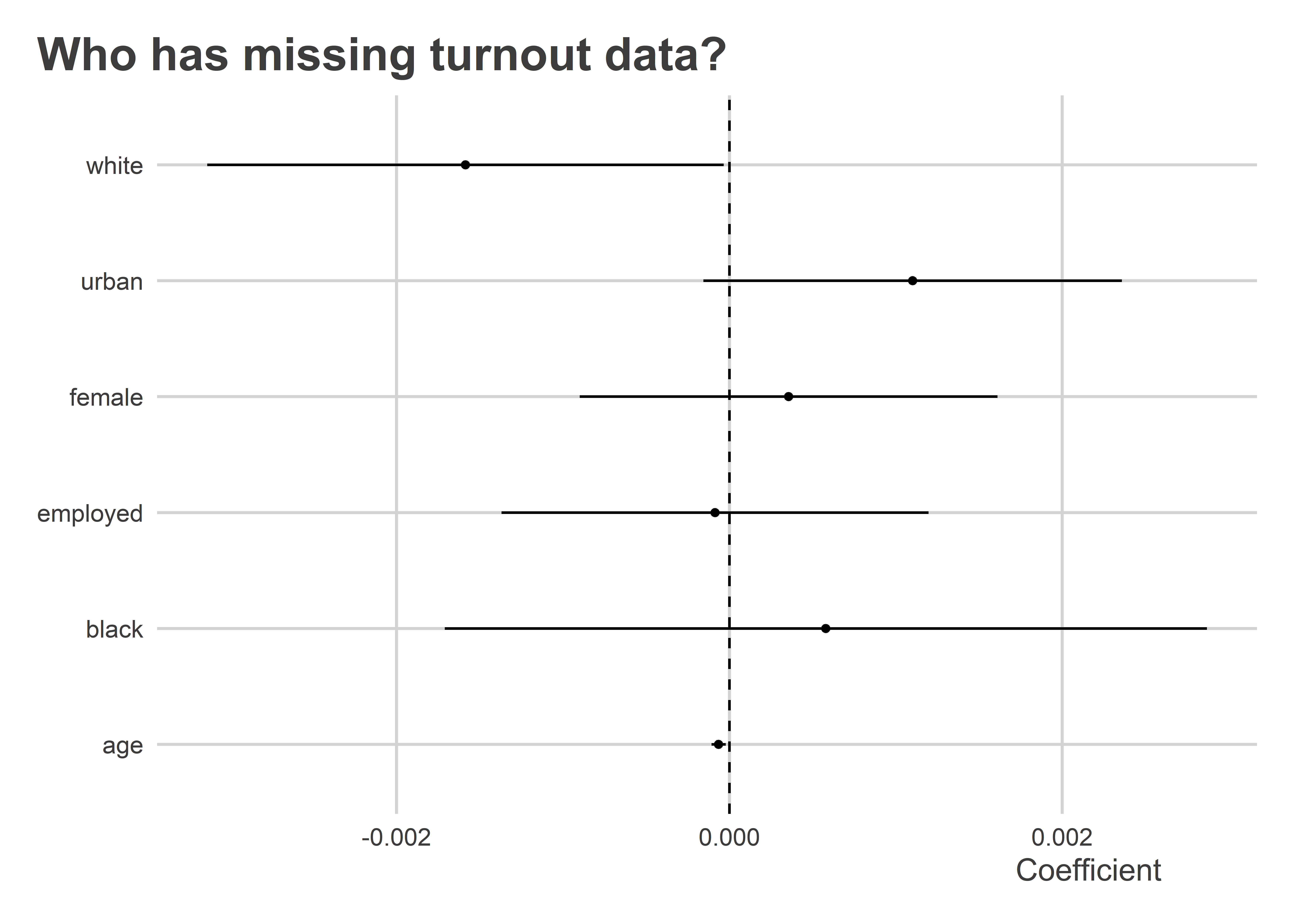
12.7 We barely scratched the surface
There is so much more that we could discuss with respect to RCTs. But we have to learn to crawl before we can run, and the above discuss has already provided plenty to think about.