library(tidyverse)
library(geomtextpath)
library(coolorrr)
library(estimatr)
library(texreg)
set_theme()
set_palette(
binary = c("red3", "steelblue")
)15 Difference-in-Differences Designs
15.1 Goals
- When treatment status changes over time for some observations but not others, we can possibly use a difference-in-differences or D-in-D design.
- D-in-D designs let us control for unobservable observation-specific and time-specific confounders.
- But, D-in-D designs require some assumptions to be met.
What you’ll need to run the code in these notes:
15.2 What’s the difference in the differences?
In the previous chapter we talked about regression discontinuity designs (RDDs). These are a kind of quasi-experimental design (QED) that let us take advantage of plausibly random treatment assignment at or near a point of discontinuity or threshold for some continuous running variable that determines who does and doesn’t get treatment. In this chapter we’ll talk about another kind of QED. It’s called a difference-in-differences or D-in-D design.
The D-in-D design has a lot in common with RDDs. The main difference is that when we get to the discontinuity in the running variable, some units receive treatment but others do not.
This kind of design is helpful if we want to know whether some policy affected outcomes. Whether the unit of observation is a city, US state, or a country, if we can find some places that implemented a policy and others that didn’t, we can compare outcomes pre- and post-policy change using places that didn’t implement the change as our “control” group.
The difference-in-differences part of the design comes from the fact that we are comparing differences in trends; not just differences in means. Here’s a data visualization (and the code to produce it) to illustrate:
DinD_data <-
tibble(
x = c(1, 2, 1, 2, 1, 2),
y = c(1, 2, 1.5, 3, 1.5, 2.5),
tr = c("No", "No", "Yes", "Yes", "Yes", "Yes"),
label = c("Control", "Control", "Treated", "Treated",
"Counterfactual", "Counterfactual")
)
ggplot(DinD_data) +
aes(
x = x,
y = y,
color = tr,
label = label
) +
geom_point(
show.legend = F
) +
geom_textline(
aes(
linetype = label,
group = label
),
show.legend = F
) +
ggpal("binary") +
scale_x_continuous(
breaks = 1:2,
labels = c("Time t", "Time t + 1"),
limits = c(0.75, 2.25)
) +
labs(
x = "Time",
y = "Outcomes",
title = "Parallel Trends and the D-in-D Design"
) +
annotate(
"text",
x = 2,
y = 2.75,
label = "''%<-%'ATE'",
hjust = -0.1,
parse = T
)
The idea is that at time t, all units are untreated. But at t + 1 some get treatment and others don’t. The difference in the change from t to t + 1 between treated and control units at t + 1 is our estimate of the treatment effect.
To put it more formally, our D-in-D design helps us to arrive at the following estimate:
First, calculate the difference over time for the control group:
\[ \delta_0 = Y_{0t+1} - Y_{0t} \]
Then, calculate the difference over time for the treated group:
\[ \delta_1 = Y_{1t+1} - Y_{1t} \]
Finally, calculate the difference in the differences:
\[ \delta_\text{D-in-D} = \delta_1 - \delta_0 \]
This difference in the trend rather than the raw difference in means between treatment and control is our estimate of the treatment effect. This approach helps us to account for background characteristics of units that might otherwise explain outcomes. For example, if you look at the figure above, notice that the control unit has a different baseline level of the outcome than the treatment unit. Right of the bat, we can see that these units are different from each other, so simply calculating a naive difference in means due to treatment isn’t going to reflect an apples-to-apples comparison. Notice, too, that the outcome changes over time for both groups as well. A D-in-D design also lets us acount for securlar changes over time. The end result is an unbiased estimate of the treatment effect.
15.3 The Standard D-in-D Design
The classical D-in-D design involves a study where we have some treated units, some untreated units, and two time periods (one pre-treatment and the other post-treatment).
We can simulate a simple example:
set.seed(111)
t <- 0:1
Y0 <- rnorm(1000) + t
Y1 <- 1 + rnorm(1000) + t*1.75
dt <- tibble(
Y = c(Y0, Y1),
D = rep(0:1, each = 1000)* (t == 1),
t = rep(t, len = 2000),
i = rep(1:1000, each = 2)
)To get the D-in-D estimate, we can use a regression framework to regress the outcome on treatment status with fixed effects for the time period (t = 0 or t = 1) and the individual unit of observation (i = 1, 2, 3, etc.). This approach helps us to adjust for:
- Time-invariant background characteristics of individuals that might influence outcomes
- The average trend in outcomes for all units
Using lm_robust(), we can implement it like this:
DinD_fit <- lm_robust(
Y ~ D,
data = dt,
fixed_effects = ~ i + t,
se_type = "stata"
)
screenreg(DinD_fit, include.ci = F)
======================
Model 1
----------------------
D 0.73 ***
(0.09)
----------------------
R^2 0.75
Adj. R^2 0.50
Num. obs. 2000
RMSE 0.98
======================
*** p < 0.001; ** p < 0.01; * p < 0.05In our simulate, the true D-in-D = 0.75. The estimate we obtain from the above is pretty close: 0.73.
Bueno de Mesquita and Fowler (2021) talk about a couple of other approaches for arriving at this same estimate. However, these approaches have limited applicability since they only will work in the the classic D-in-D design setup with multiple units of observation but only two periods. The regression framework applied above, however, easily generalizes to cases with more than just two periods.
15.4 The Generalized D-in-D Design
When we’re dealing with data that has more than a couple time periods corresponding with the timing of treatment, we use what’s called a generalized D-in-D design, so called because we’re generalizing the design to be more flexible to different kinds of data.
The approach is quite similar the regression framework applied above, but with a few key considerations. To illustrate, let’s look at some US Congressional data. You can read more about what’s in the data it here: README
congress_dt <- read_csv(
"https://raw.githubusercontent.com/milesdwilliams15/Teaching/main/DPR%20201/Data/CongressionalData.csv"
)Say we wanted to know the effect of party membership on voting behavior. We did this before using a simple SOO approach, but with the congress_dt data we can use a D-in-D design. The reason is that we observe different congressional districts over time, and for each we have data on the partisan ID of congress members and how conservatively they voted. By calculating the difference in the differences over time in how conservatively the member of congress votes if a different party comes into power in a district, we can estimate the effect of party ID on voting behavior.
To implement the D-in-D design we’ll use lm_robust() and set up the main formula object as cvp ~ republican. We’ll also include the congress session and district ID as fixed effects:
cong_DinD_fit <- lm_robust(
cvp ~ republican,
data = congress_dt,
fixed_effects = ~ state_dist + cong,
se_type = "stata"
)
screenreg(cong_DinD_fit, include.ci = F)
=======================
Model 1
-----------------------
republican 0.46 ***
(0.01)
-----------------------
R^2 0.98
Adj. R^2 0.97
Num. obs. 2074
RMSE 0.05
=======================
*** p < 0.001; ** p < 0.01; * p < 0.05The D-in-D estimate tells us that Republican members of Congress are 46 percentage points more likely to vote in a conservative way compared to Democrats. This is only slightly different from what we’d see if we just took a simple difference in means due to party ID:
lm_robust(
cvp ~ republican,
data = congress_dt,
se_type = "stata"
) |>
screenreg(
include.ci = F
)
========================
Model 1
------------------------
(Intercept) -0.28 ***
(0.01)
republican 0.48 ***
(0.01)
------------------------
R^2 0.56
Adj. R^2 0.56
Num. obs. 2074
RMSE 0.21
========================
*** p < 0.001; ** p < 0.01; * p < 0.05Now something you should be asking yourself right about now is: how can we be sure that we’ve appropriately dealt with omitted variable bias? Shouldn’t we adjust for something like ideology like we did in the SOO chapter? Let’s consider really quickly what we need to assume is true to trust the D-in-D estimate.
15.5 Checking Pre-Trends
Like all QEDs the D-in-D design is powerful, but it relies on certain identifying assumptions—i.e., things we need to be true for the D-in-D estimate to be unbiased.
The key assumption with D-in-D designs is the parallel trends assumption. This idea was captured with the first figure produced in these notes. In order to be sure that a policy intervention is the cause of changes in an outcome, we need to be convinced that both treated and untreated units would have had the same post-treatment trend absent the intervention.
Knowing whether parallel trends holds post-treatment is impossible. But we can at least get some reassurance by checking pre-treatment trends. Take our data above:
ggplot(congress_dt) +
aes(
x = cong,
y = cvp,
color = ifelse(republican == 1, "1. Rep.", "2. Dem")
) +
geom_line(
aes(group = state_dist),
alpha = 0.3
) +
geom_point() +
labs(
x = "Congress Session",
y = "Conservative Vote\n(Probability Margin)",
color = NULL
) +
ggpal("binary")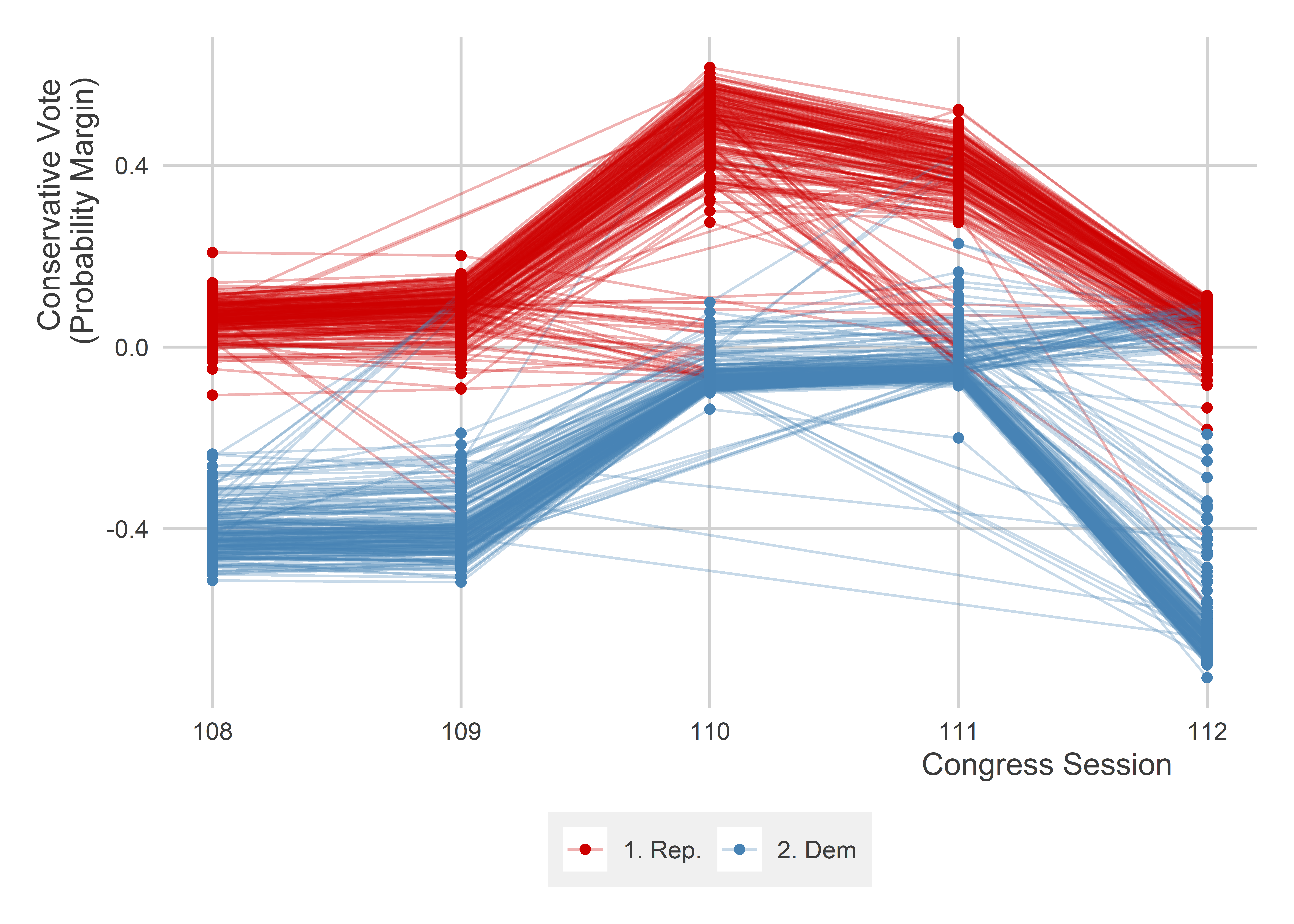
In the above our D-in-D design is helping us to identify whether a shift in the voting behavior of a congress member from a particular district is due simply to an average trend in voting for that district or due to the partisanship of the person in office. It seems that generally from one session of congress to the next, the trend remains roughly parallel and the biggest changes come from seats where we observe a change in party control of the seat. This provides some reassurance about the parallel trends assumption.
Importantly, the fact that parallel trends are observable in the past does not guarantee that it holds under treatment. The fundamental problem of causal inference is an ever-present reality in data-driven research.
15.6 Dangers with generalized D-in-D designs
One important note of caution is warranted with the generalized D-in-D. The kind of regression model that we use in such a design is called a two-way fixed effects (TWFE) regression. When there are many time periods and there’s some inconsistency in the timing of treatment (like what we observe in the congressional voting data), some weird things can happen “under the hood.”
For example, it is possible that the introduction of TWFEs in the model will generate negative weights for treatment. Let me show you what this means. Remember how with SOO designs when we control for covariates, we’re effectively generating predictions for the outcome variable and causal variable as a function of these covariates, and then we’re using the left-over variation in these variables after subtracting out these predicted values to estimate the causal effect of interest. We’re basically doing the same thing with TWFEs, but in this case these fixed effects are our predictor variables for treatment and response rather than a set of observed covariates.
Check it out. The below code regresses cvp and republican on the congress session and state district fixed effects and pulls out the residual variation in each from each regression (that’s the variation left over that isn’t accurately predicted by these fixed effects). It then takes this left over variation and estimates the D-in-D effect. Notice that the estimate is identical to the TWFE regression estimated in the previous section.
cvp_res <- lm(
cvp ~ as.factor(cong) +
as.factor(state_dist),
data = congress_dt
) |> resid()
rep_res <- lm(
republican ~ as.factor(cong) +
as.factor(state_dist),
data = congress_dt
) |> resid()
lm_robust(
cvp_res ~ rep_res,
se_type = "stata"
) |>
screenreg(
include.ci = F
)
========================
Model 1
------------------------
(Intercept) -0.00
(0.00)
rep_res 0.46 ***
(0.01)
------------------------
R^2 0.78
Adj. R^2 0.78
Num. obs. 2074
RMSE 0.05
========================
*** p < 0.001; ** p < 0.01; * p < 0.05One thing that’s weird about this research design is that treatment assignment (whether a Republican or Democrat is in office in a given district) is not constant over time. Different districts receive treatment at different points in time, and some actually go back and forth between being treated and not. This is just the kind of scenario that could lead us to get some negative treatment weights. These negative weights arise if the TWFE regression of treatment on the fixed effects gives us cases where a unit is treated but its predicted treatment is erroneously greater than 1. This is nonsensical, because treatment can only be 0 or 1, and the probability of getting treatment can’t be less than 0 or greater than 1. But sometimes linear regression models will give us predictions outside these bounds when we have a binary outcome.
To check whether this is going on, the below code adds the residual Republican indicator to the congress dataset and then groups it by Republican status and calculates the share of the time that the residual for being a Republican is negative. The output tells us that almost 46% of the time when a district has a Republican in office, the residual for the Republican indicator is negative. Even more, we see the reverse problem for Democratic districts. Almost 70% of the time the residual is positive when a district is Democrat controlled. This means a bunch of control observations are getting a positive treatment weight, but a bunch of treated observations are getting a negative treatment weight. This doesn’t necessarily mean that our estimate of the treatment effect with the D-in-D is biased, but it’s concerning.
congress_dt |>
mutate(
rep_res = rep_res
) |>
group_by(
republican
) |>
summarize(
mean = mean(rep_res < 0)
)# A tibble: 2 × 2
republican mean
<dbl> <dbl>
1 0 0.682
2 1 0.458To further help illustrate what’s going on, remember the equation we use to estimate the slope coefficient in a regression model? With our left-over variation in the data above, we can simply calculate the difference in voting behavior due to a difference in party ID as:
\[ \hat \delta_\text{D-in-D} = \frac{\text{cov}(\tilde y_i, \tilde x_i)}{\text{var}(\tilde x_i)} \]
where
\[ \begin{aligned} \tilde y_i & = y_i - \hat y_i \\ \tilde x_i & = x_i - \hat y_i \end{aligned} \]
The variable \(y\) represents how conservatively a candidate votes, \(\hat y\) represents how conservatively they are predicted to vote depending on the session of congress and their district ID, and \(\tilde y\) is the difference between the two. The variable \(x\) is the binary indicator for whether a district has a Republican member during a session of congress, \(\hat x\) is a predicted probability that district’s candidate is a Republican, and \(\tilde x\) is the difference between the two.
Something to note about the formula for a regression coefficient is that you can get the same estimate for it by writing the equation like this:
\[ \hat \delta_\text{D-in-D} = \frac{\sum_{i = 1}^n\tilde x_i \tilde y_i}{\sum_{i = 1}^n \tilde x_i^2} \]
If we break this summation down to just the value for a given observation, we have the following observation specific estimate of \(\delta\):
\[ \hat \delta_i = \frac{\tilde y_i}{\tilde x_i} \]
In all cases where \(i\) gets treatment but the TWFE estimator generates a fitted \(\hat x_i\) that is greater than 1, \(\tilde x_i\) will be negative. This means if the outcome for \(i\) is greater than what would be predicted based on the set of unit and time fixed effects, it will look like the difference due to treatment is negative for this given observation.
Again, let’s see if visualizing this problem helps. The below code generates a scatter plot using the leftover variation in Republican ID and conservative voting. While in the raw data, Republican ID is a binary variable, the process of adjusting for time and congressional district gives us a residualized version of the measure that is continuous. If we look at the data, it’s clear that a positive relationship exists between the leftover variation in these variables. However, notice what’s going on in the center of the figure. I’ve highlighted the data points in the middle of the scatter plot using a box to show that something weird is going on. We have some odd mixing of data points. There are some districts with Republican members of congress that have a negative value when adjusting for TWFEs, and there are some Democratic members of congress that have a positive value when adjusting for TWFEs. In both cases, this is happening because the TWFE estimator is give us bad predictions of the likelihood of Republican party ID (that is, estimated probabilities that are either greater than 1 or less than 0).
congress_dt |>
mutate(
rep_res = rep_res,
cvp_res = cvp_res
) |>
ggplot() +
aes(
x = rep_res,
y = cvp_res,
color = republican==0
) +
geom_point(
alpha = 0.5
) +
geom_vline(
xintercept = 0,
linetype = 2
) +
ggpal(
"binary",
labels = c("Rep", "Dem")
) +
labs(
x = "Leftover Variation in Republican ID",
y = "Leftover Variation in Voting",
color = "Party ID"
) +
geom_rect(
aes(xmin = -.15,
xmax = .15,
ymin = -.15,
ymax = .15),
alpha = 0,
color = "black"
) +
annotate(
"text",
x = .15,
y = -.1,
label = "''%<-%'Party ID Mixed'",
hjust = -.1,
parse = T
)
To better see how this creates an issue, the next data viz below zooms in on the data points in this box and for each it plots the observation specific difference-in-differences effect or slope. Overlayed on top of this is an overall regression slope estimate. What you can see is that several observations with Republican IDs have a negative slope. The reason is that these observations have a negative residual value. Nonetheless, their level of conservative voting has a positive residual, indicating that these members are voting more conservatively than expected based on the TWFE predictions. We see the inverse problem for a number of Democratic districts.
congress_dt |>
mutate(
rep_res = rep_res,
cvp_res = cvp_res
) |>
filter(
between(rep_res, -.15, .15),
between(cvp_res, -.15, .15)
) |>
ggplot() +
aes(
x = rep_res,
y = cvp_res,
color = republican==0
) +
geom_abline(
aes(
color = republican == 0,
intercept = 0,
slope = cvp_res / rep_res
),
alpha = 0.1
) +
geom_point(
alpha = 0.5
) +
geom_vline(
xintercept = 0,
linetype = 2
) +
geom_smooth(
method = "lm",
se = F,
color = "black"
) +
ggpal(
"binary",
labels = c("Rep", "Dem")
) +
labs(
x = "Leftover Variation in Republican ID",
y = "Leftover Variation in Voting",
color = "Party ID",
title = "Check out the negative weights generated\nwith TWFEs"
) 
Now, whether this odd weighting problem really is a source of bias depends on how many observations are affected and whether the problem is symmetrical. However, even when it occurs in small quantities, it suggests that something is improper about the way the TWFE estimator is working. There have been a number of recent advances with TWFEs that developers claim can get around these weighting issues. These methods are beyond the scope of this chapter, but those interested may want to check out options such as the “extended” TWFE method, which you can learn more about here: https://cran.r-project.org/web/packages/etwfe/vignettes/etwfe.html
15.7 Conclusion
D-in-D designs are really useful, but we do need to make some assumptions about the data to trust the results we get from this approach. The main assumption we need to be concerned about is the parallel trends assumption. We also need to cautious of generalizing the D-in-D to multiple time periods. With this kind of data, if treatment assignment is inconsistent, it’s possible that the TWFEs we need to include in the model will give us nonsensical weights on the treatment indicator. It’s very simple to check if this is going on, but knowing whether and how much this problem results in bias is impossible to know with certainty.