13 Selection on Observables

13.1 Goals

Randomized experiments are ideal for making causal inferences.
But sometimes, experiments aren’t feasible for logistical or ethical reasons.
Our next best option is to use data from a non-experiment (real-world events like civil wars, elections, protests) and try to control for observed confounders.
Thinking about a theoretical model of causation can help guide our design.
This won’t solve all our problems, because we can only control for what we can observe or measure.
Any unobserved confounders can still be lurking under the surface of our data.

13.2 When Experiments Aren’t an Option

You probably have heard of people “controlling” for different factors in a statistical analysis. What they usually mean by this is that they’ve included a bunch of different factors in a regression model to adjust for the confounding influence of these factors on the relationship between an explanatory or causal variable of interest and an outcome. When done well, this approach can help to reduce bias and improve statistical precision. When done poorly, it can make one or both of these problems worse.

A research design where we control for variables in a regression analysis is sometimes referred to as selection on observables (SOO). The idea is that there are a number of observed factors or characteristics of observations in our data that predict or determine who does or doesn’t get “treated” by a causal variable of interest. We should use the term “treated” loosely, because in an SOO design we’re not dealing with an experimental study where treatment assignment is random. However, assuming we have sufficient data to explain why a causal variable is distributed/assigned the way that it is, an SOO design allows us to draw out variation in this causal variable that is random, which we can then use to estimate its causal effect.

Regression analysis is the most commonly used tool for SOO, and in many cases it works just fine. However, we have to rely on a few assumptions to make the most of this research design. The following sections walk through some issues you need to consider when controlling for covariates in a regression analysis. Among the many lessons I hope you take away from this discussion is that there is no magic solution to the problem of confounding in non-experimental data. When our data are observational, we often don’t really know the true process that generated them. We may have some theories, but these theories are always contingent and subject to change. For this reason, many SOO designs are heavily susceptible to researcher degrees of freedom and, even worse, p-hacking. The choice to include or exclude certain factors as control variables can lead to drastically different conclusions about causal effects. To make things even more complicated, it is possible that many different regression model specifications are perfectly and equally justifiable. This leaves us with no objective basis for adjudicating between one model or another.

The lesson here is not to avoid SOO research designs. Rather, it is to be clear-eyed about the limitations of SOO and to treat the results from your analysis with the appropriate level of caution.

13.3 Motivating SOO Designs with DAGs

A directed acyclic graph or DAG is a useful way of visualizing both simple and complex causal relationships between variables when we want to use an SOO design. By using DAGs, we can start to think more clearly about our data and what variables we think we need to control for (and not control for) in our analysis.

Visualizing a DAG in R is really easy with the {ggdag} package, which you can install by writing:

install.packages("ggdag")

We’ll make an example DAG that summarizes the theoretical causal relationship among three variables: Voting, Ideology, and Party Membership in the U.S. Congress.

First open the {tidyverse} along with {ggdag}:

library(tidyverse)
library(ggdag)
library(estimatr)
library(coolorrr)
set_theme()
set_palette()

Next, to make a DAG you’ll give R some instructions about the relationships between variables using dagify(). You can then pipe these instructions to ggdag(). The below code does so and adds some customization along the way:

dagify("Voting" ~ "Ideology" + "Party",
       "Party" ~ "Ideology") |>
  ggdag(
    text_col = "steelblue",
    node = F,
    text_size = 5,
    edge_type = "diagonal"
  ) +
  theme_dag() +
  labs(
    title = "Hypothetical causal model of US Congress voting behavior",
    caption = "(Direction of arrows denotes direction of causation)"
  )

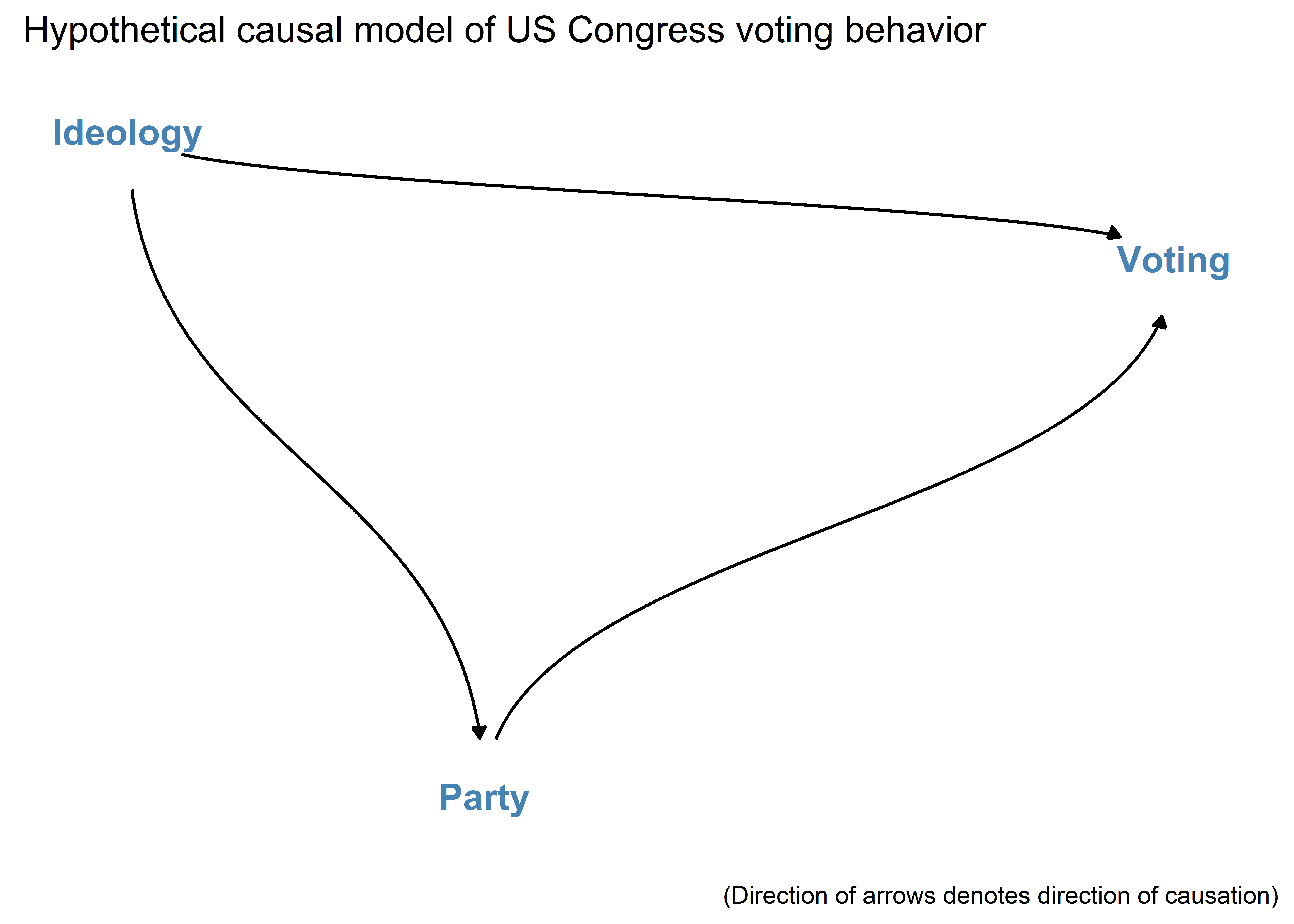
The above represents a theoretical model of the causal relationships between political ideology, partisanship, and voting behavior in Congress. Specifically, it argues that ideology influences how individuals vote and their party ID, and that party ID in turn also influences how individuals vote.

We can simulate some data based on this model:

dt <- tibble(
  ideology = c(
    rep(1, len = 70),
    rep(2, len = 70),
    rep(3, len = 69),
    rep(4, len = 70),
    rep(5, len = 70)
  ),
  republican = randomizr::block_ra(
    blocks = ideology,
    block_m = c(0, 4, 45, 69, 69)
  ),
  voting = republican + ideology + rnorm(length(ideology))
) |>
  mutate(
    voting = 100 * (voting - min(voting)) / (max(voting) - min(voting))
  )

If we look at the raw data, we can see a clear positive relationship between party ID (republican) and voting behavior (voting). The outcome here is meant to be the share of times a member of Congress voted in a way that was consistent with conservative ideology. It should be unsurprising that more Republicans are conservative than Democrats, so this is probably driving some of the relationship we see in the data. But is ideology all there is to it? Our causal DAG tells us that a mix of party ID and ideology influence voting. However, since it also tells us that ideology influences party membership, we should be careful about drawing conclusions from looking at the raw data. The reasons why someone is a Republican or a Democrat are not random.

ggplot(dt) +
  aes(
    x = republican,
    y = voting
  ) +
  geom_point(
    alpha = 0.3
  ) +
  geom_smooth(
    method = "lm",
    se = F,
    color = "steelblue"
  ) +
  scale_x_continuous(
    breaks = 0:1,
    labels = c("Democrat", "Republican")
  ) +
  labs(
    x = NULL,
    y = "% Conservative Votes"
  )

Assuming we didn’t know anything about how our data were generated, a skeptic could make the argument that the relationship between partisanship and voting is spurious. People pick which party they belong to on the basis of their ideology, and their ideology also determines how they vote. So the observed relationship between party ID and voting could just be a reflection of this underlying behavior.

However, an alternative argument can be made that partisanship, even though it is partly explained by ideology, still has a direct effect on voting. The mechanism driving this might be partisan peer-pressure. Once someone is in Congress, they may face strong pressure to conform to the party line. This can create an extra incentive, on top of ideology, to vote in a certain way.

Both of the above arguments sound plausible, and the best way to adjudicate between them is to control for ideology in our analysis. If the first argument is true, once we adjust for ideology in our research design, party ID should no longer be a statistically significant predictor of voting. However, if the alternative argument is true, we should still see a significant relationship between party ID and voting even after ideology is adjusted for.

We can estimate a pair of regression models to see how controlling for ideology changes our inferences about party ID. The below code uses lm_robust() and uses HC1 robust standard errors to determine statistical significance. Note that these are the same standard errors that we talked about in a previous chapter that are analogous to bootstrapping. In non-RCT research designs, we usually cannot fully justify randomization-based inference, so we have to revert back to sampling-based inference instead.

# A simple regression model
fit1 <- lm_robust(voting ~ republican, dt, se_type = "stata")

# A multiple regression model that controls for ideology
fit2 <- lm_robust(voting ~ republican + ideology, dt, se_type = "stata")

# show results
library(texreg)
screenreg(
  list(
    fit1, fit2
  ),
  include.ci = F
)


===================================
             Model 1     Model 2   
-----------------------------------
(Intercept)   27.00 ***    7.94 ***
              (1.07)      (1.45)   
republican    35.06 ***    9.54 ***
              (1.49)      (2.06)   
ideology                  10.91 ***
                          (0.69)   
-----------------------------------
R^2            0.61        0.77    
Adj. R^2       0.61        0.77    
Num. obs.    349         349       
RMSE          13.89       10.77    
===================================
*** p < 0.001; ** p < 0.01; * p < 0.05

When we estimate the first model, we clearly see that partisan ID is a strong predictor of voting. Specifically, being Republican increases conservative voting behavior by 35.06 percentage points. However, once ideology is controlled for, the estimated effect of party ID shrinks to 9.54 percentage points. Both estimates are statistically significant, but the first is inflated because we haven’t accounted for the role that ideology plays, both in driving voting and in driving party membership.

This inflated result in the first regression model is a product of a special kind of bias called omitted variable bias. The idea is that, by failing to control for a confounding variable, estimates of a causal relationship of interest can deviate systematically from the truth. The next section walks through how we can measure this bias depending on its particular source.

13.4 Measuring Bias

There are four general scenarios that influence the direction of the bias in a study with confounding. If the confounder is omitted from the analysis, it will result in the following biases:

If the omitted variable has a positive correlation with treatment and the outcome, the bias will be positive (this is what we saw in the example in the previous section)
If the omitted variable has a positive correlation with treatment and a negative correlation with the outcome, the bias will be negative
If the omitted variable has a negative correlation with treatment and a positive correlation with the outcome, the bias will be negative
If the omitted variable has a negative relationship with the treatment and the outcome, the bias will be positive

We can do a simple simulation to illustrate:

d1 <- tibble(
  z = rnorm(1000),
  x = z + rnorm(1000),
  y = z + x + rnorm(1000)
)
d2 <- tibble(
  z = rnorm(1000),
  x = -z + rnorm(1000),
  y = z + x + rnorm(1000)
)
d3 <- tibble(
  z = rnorm(1000),
  x = z + rnorm(1000),
  y = -z + x + rnorm(1000)
)
d4 <- tibble(
  z = rnorm(1000),
  x = -z + rnorm(1000),
  y = -z + x + rnorm(1000)
)

Each of these datasets is going to give us a different direction of bias. To calculate the bias we’ll first need to estimate some simple regression models:

sf <- y ~ x
s1 <- lm(sf, d1)
s2 <- lm(sf, d2)
s3 <- lm(sf, d3)
s4 <- lm(sf, d4)

We’re then going to estimate the full (correct) regression models:

mf <- y ~ x + z
m1 <- lm(mf, d1)
m2 <- lm(mf, d2)
m3 <- lm(mf, d3)
m4 <- lm(mf, d4)

If we use screenreg() from {texreg} to summarize the output of these models, we can clearly see that the simple models have different estimates for the effect x on y than the full models:

screenreg(list(s1, s2, s3, s4),
          include.ci = F)


===============================================================
             Model 1      Model 2      Model 3      Model 4    
---------------------------------------------------------------
(Intercept)     0.04         0.03         0.02         0.03    
               (0.04)       (0.04)       (0.04)       (0.04)   
x               1.50 ***     0.56 ***     0.54 ***     1.50 ***
               (0.03)       (0.03)       (0.03)       (0.03)   
---------------------------------------------------------------
R^2             0.75         0.32         0.28         0.78    
Adj. R^2        0.75         0.31         0.28         0.78    
Num. obs.    1000         1000         1000         1000       
===============================================================
*** p < 0.001; ** p < 0.01; * p < 0.05

screenreg(list(m1, m2, m3, m4),
          include.ci = F)


===============================================================
             Model 1      Model 2      Model 3      Model 4    
---------------------------------------------------------------
(Intercept)     0.03         0.02         0.03         0.03    
               (0.03)       (0.03)       (0.03)       (0.03)   
x               1.01 ***     1.02 ***     1.00 ***     1.03 ***
               (0.03)       (0.03)       (0.03)       (0.03)   
z               1.01 ***     0.95 ***    -0.99 ***    -0.93 ***
               (0.04)       (0.04)       (0.04)       (0.05)   
---------------------------------------------------------------
R^2             0.84         0.53         0.52         0.85    
Adj. R^2        0.84         0.53         0.52         0.85    
Num. obs.    1000         1000         1000         1000       
===============================================================
*** p < 0.001; ** p < 0.01; * p < 0.05

Does it look like the bias runs in the expected directions?

We’ll make a simple function that lets us calculate the bias:

bias <- function(s, m) {
  bias <- coef(s)["x"] - coef(m)["x"]
  bias # return bias
}

Now we can use it:

bias(s1, m1) # y = +z; x = +z

        x 
0.4973238

bias(s2, m2) # y = +z; x = -z

         x 
-0.4627276

bias(s3, m3) # y = -z; x = +z

         x 
-0.4582887

bias(s4, m4) # y = -z; x = -z

        x 
0.4767473

The answer is yes. Unfortunately, in real-world settings doing this kind of exercise is difficult because you don’t know for sure what the true data-generating process was that gave rise to your observational data. However, the ability to perform a simulation like this can help us understand how omitted variable bias can be at work. It can also help us to speculate about the direction of bias in our studies. A problem in many SOO designs is that we often can’t measure all possible confounding variables. If we think of a confounder that we think is important but that we don’t have data for, if we know what its expected relationship would be with the outcome and causal variable of interest, we can at least make an informed guess about whether our estimate is biased upward or downward.

13.5 How does regression control?

So we can use regression models to control for confounders, but what does it really mean to control for something? As we’ve seen, including a confounding variable in our regression model changes our estimate for the causal variable of interest. Let’s look “under the hood” of regression models for a second to see how controlling for factors changes our estimates.

Let’s go back to our simulated ideology, partisanship, and voting data. Let’s visualize the relationship between ideology and voting:

set_palette(
  binary = c("steelblue", "red3")
)
p <- ggplot(dt) +
  aes(x = ideology, 
      y = voting) +
  geom_jitter(
    aes(color = ifelse(republican == 1, "Rep.", "Dem.")),
    width = .1,
    alpha = 0.4
  ) +
  ggpal(type = "binary") +
  labs(x = "Conservative Ideology",
       y = "Conservative Voting Score",
       color = NULL) 
p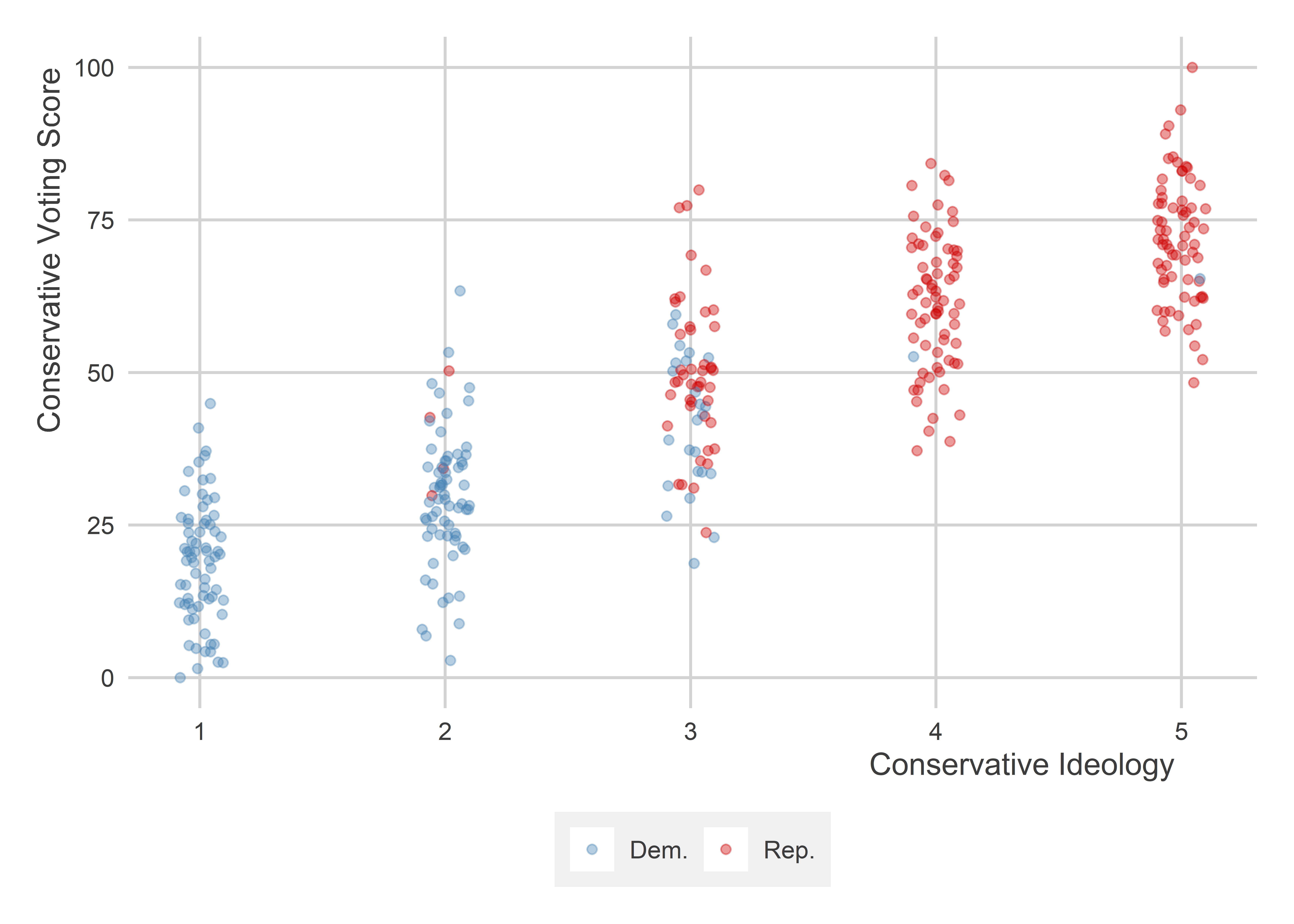

We can see from the above that conservative ideology has a positive correlation with conservative voting score. We can also see that conservative candidates are disproportionately members of the Republican party.

We could just estimate the relationship between ideology and voting with a simple model like this:

p + 
  geom_smooth(
    method = lm,
    se = F,
    color = "black"
  )

But we could also do separate models by party:

p + 
  geom_smooth(
    aes(color = ifelse(republican == 1, "Rep.", "Dem.")),
    method = lm,
    se = F
  )

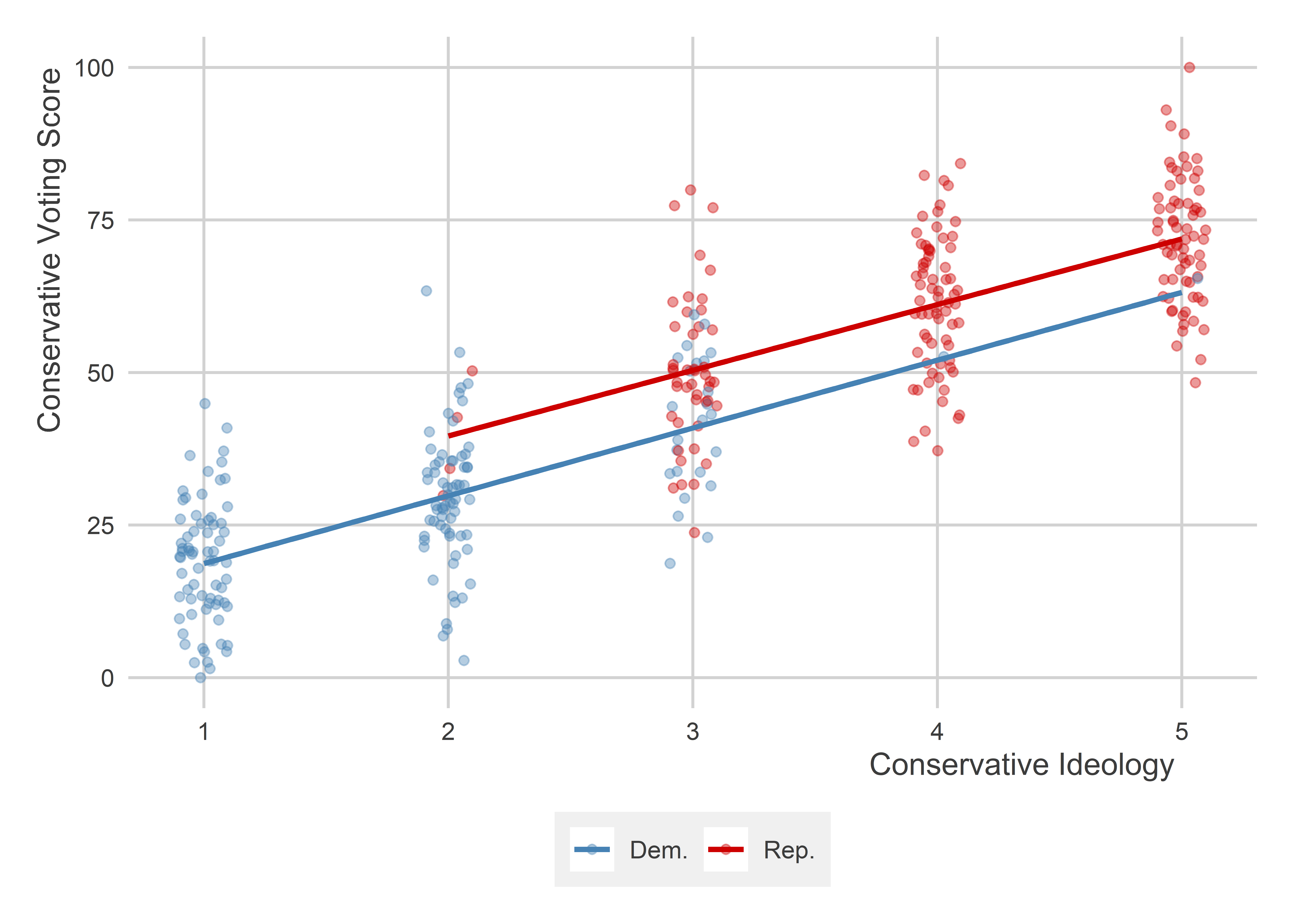
When we estimate a multiple regression model that also controls for party membership, what we effectively are doing is calculating a weighted average of both of these slopes and using that per party, instead:

p + 
  geom_line(
    aes(y = predict(lm(voting ~ ideology + republican)),
        color = ifelse(republican == 1, "Rep.", "Dem.")),
    size = 1
  )

An equivalent way to go about this is to estimate a regression model in stages. Keeping with the above example, if we want to estimate the effect of partisanship on voting while controlling for ideology, we could start by estimating the following regression models:

## step 1: fit voting ~ ideology
step1 <- lm(voting ~ ideology, dt)

## step 2: fit republican ~ ideology
step2 <- lm(republican ~ ideology, dt)

The first model above is just a simple regression of voting on ideology. The second is a simple regression of republican ID and ideology. The next step we’ll take is to pull out the residuals from these regression models and save them. Remember that residuals are the difference between model predictions and the true observed values of the data. Residuals are the unexplained variation in our data left over after modeling some variable as a function of a predictor or set of predictors.

## step 3: get residuals
voting_res <- resid(step1)
republican_res <- resid(step2)

The final step will be to regress the left-over (residual) variation in voting on the left-over (residual) variation in party ID. The coefficient for this relationship will be our estimate of the effect of party ID on voting, controlling for ideology. If we compare this fit to fit2 which we estimated early in this chapter, we should observe that the estimates for party ID are the same.

res_fit <- lm_robust(voting_res ~ republican_res, se_type = "stata")
screenreg(
  list(
    fit2, res_fit
  ),
  include.ci = F
)


======================================
                Model 1     Model 2   
--------------------------------------
(Intercept)       7.94 ***   -0.00    
                 (1.45)      (0.58)   
republican        9.54 ***            
                 (2.06)               
ideology         10.91 ***            
                 (0.69)               
republican_res                9.54 ***
                             (2.05)   
--------------------------------------
R^2               0.77        0.06    
Adj. R^2          0.77        0.06    
Num. obs.       349         349       
RMSE             10.77       10.76    
======================================
*** p < 0.001; ** p < 0.01; * p < 0.05

What I like about this way of controlling for covariates is that it makes it really clear that we’re making an additional set of assumptions by using regression models to adjust for confounders. Under the hood, we’re assuming that the confounder or confounders make for a good linear model of both the outcome variable and the causal variable of interest. If a linear model isn’t a good fit in either case, we could actually make bias worse rather than better by controlling for a confounder.

Here’s some simulated data based on a classic example of this problem from the political scientist Christopher Achen which we talks about in a provocatively titled article called “Let’s Put Garbage-Can Regressions and Garbage-Can Probits Where They Belong.”

tibble(
  x1 = seq(0, 1, by = 0.1),
  x1_obs = round(x1^2, 1),
  x2 = round(sqrt(x1)/3, 1),
  y = x1 - 0.1 * x2
) -> dt

## look at the data
dt |>
  kableExtra::kbl(
    caption = "Example Data"
  )

Example Data
x1	x1_obs	x2	y
0.0	0.0	0.0	0.00
0.1	0.0	0.1	0.09
0.2	0.0	0.1	0.19
0.3	0.1	0.2	0.28
0.4	0.2	0.2	0.38
0.5	0.2	0.2	0.48
0.6	0.4	0.3	0.57
0.7	0.5	0.3	0.67
0.8	0.6	0.3	0.77
0.9	0.8	0.3	0.87
1.0	1.0	0.3	0.97

This hypothetical data assumes a true data-generating process for an outcome that looks like this:

\[ y_i = x_{1i} - 0.1 \times x_{2_i} \]

However, it throws a curve ball at us. It assumes that we don’t observe \(x_{1i}\) but a version of it called \(\hat x_{1i}\). This observed version is correlated with the true version, but the relationship is not perfectly linear. It is monotonic, which just means that it is a positive relationship through-and-through. But if we look at the relationship between the observed and actual values of this variable, we can see a clear discrepancy.

ggplot(dt) +
  aes(
    x = x1,
    y = x1_obs
  ) +
  geom_point(
    color = "red3"
  ) +
  geom_smooth(
    se = F,
    color = "steelblue"
  ) + 
  labs(
    x = expression("True "*x[1]),
    y = expression("Observed "*x[1]),
    title = "The observed data is not a perfect linear function of the\ntrue underlying factor"
  )

Suppose we want to estimate the effect of \(x_{2i}\) on \(y_i\). Based on the way the data were generated, we know that this variable has an effect of -0.1 on the outcome, but we also know that it is correlated with \(x_{1i}\). So if we just try to estimate the direct effect of this variable on the outcome, we’ll get a biased result (an estimate of 2.833):

lm(y ~ x2, dt)


Call:
lm(formula = y ~ x2, data = dt)

Coefficients:
(Intercept)           x2  
    -0.1133       2.8333

Even though we can’t observe \(x_{1i}\), we do have the observed version. So we should probably control for this, right? Something is better than nothing, surely. Well…

lm(y ~ x1_obs + x2, dt)


Call:
lm(formula = y ~ x1_obs + x2, data = dt)

Coefficients:
(Intercept)       x1_obs           x2  
    0.01978      0.60280      1.20075

Clearly the estimate for \(x_{2i}\) is closer to the truth, but it still is dramatically inflated in absolute magnitude and it’s in the wrong direction! What’s going on here? The simple truth is that the observed version of the confounding variable does not have a linear relationship with either the outcome or the causal variable of interest. As a result, controlling for it in a linear regression model yields biased results.

One solution to this problem is just to find better data. Check out what happens if we use the true confounder. Everything is as it should be!

lm(y ~ x1 + x2, dt)


Call:
lm(formula = y ~ x1 + x2, data = dt)

Coefficients:
(Intercept)           x1           x2  
  1.339e-16    1.000e+00   -1.000e-01

The message here is clear. Controlling for confounders is important, but it is not a magic bullet. Even if we can observe all the relevant confounders, if our data is flawed in some way, controlling for confounders can introduce a new kind of bias due to model mis-specification.

13.6 The limitations of controlling

To summarize everything we’ve covered so far, when we control for confounding covariates, we are assuming selection on observables, which is the idea that the process of treatment assignment is determined by other observed factors. As we’ve seen, our ability to remove bias from our estimate of the effect of a variable of interest on an outcome is limited by the extent to which:

We observe all the factors that influence the treatment and outcome.
We have good data on these factors.
A linear regression model is the best model for the data.

These problems haunt all observational studies, even those that control for dozens of possible confounding factors.

You can use some methods like sensitivity analysis to at least speculate about how big omitted variable bias would have to be to change the results of your study. This is a more advanced technique that we won’t cover in this class, but the curious should check out the {sensemakr} package.

Other landmines await the intrepid observational researcher. Perhaps two of the most common, aside from omitted variable bias, bad data, and model mis-specification are (1) mistaking confounders for mechanisms and (2) post-treatment bias.

An example of mistaking a confounder for a mechanism is controlling for incidence of lung cancer in a study about the effect of smoking on mortality. It should go without saying that smoking is deadly. But one of the reasons or mechanisms that explains its deadliness is its effect on the incidence of lung cancer. Obviously, if we want to estimate the effect of smoking on mortality, it doesn’t make sense to control for lung cancer, and doing so could actually bias the results.

Post-treatment bias involves controlling for a variable in your model that is also caused by the treatment but which has no true relationship with the outcome. Post-treatment bias can accidentally create spurious correlations or make other relationships disappear in the data.

None of these issues are reasons to avoid SOO as a research design. Much of my own research relies on this approach because I study issues in international politics where RCTs are practically impossible and ethically dubious. It is important, however, to be a critical consumer of observational research.

13.7 What’s the value of SOO designs if they have so many problems?

At this point you may be wondering what the value of SOO designs are if they have so many pitfalls. To be sure, we should be cautious about this kind of research design and be conservative about what conclusions we can draw. However, there is still a lot of value that can come from this approach to research. A big one is that it can help identify problems or issues where we might be interested in digging deeper to assess causality in a more rigorous way. For example, I and a colleague of mine are working on a project looking at whether there is evidence that countries that give foreign aid will punish aid recipients by cutting different kinds of assistance if the recipient regime steels money from foreign investors. We find that they do, and that the specifically cut humanitarian aid. However, we can’t go so far as to claim this is a causal relationship because theft of foreign investment is not random, and the kinds of countries that are most apt to engage in this behavior probably are differently in need of aid compared to the average country. Even so, this relationship does exist and, if it were causal, this would possibly be normatively bad because every time a country steels money from foreign investors, it’s possibly depriving its citizens of life-saving humanitarian aid. That’s a normatively weighty problem, and our hope is that by identifying this relationship we can motivate additional research on this issue.

Not all observational studies are motivated in this way, but the SOO research design can often serve as the first cut at a problem or issue that then serves as a basis for future studies.

13.8 Wrapping up

Observational studies are incredibly important and necessary for making causal inferences when logistics and ethics make it impossible to run a randomized controlled trial. But, observational studies have limitations, so you need to be clear eyed about what conclusions you can and can’t confidently draw.